Question 38 (Textile Engineering & Fibre Science)
Consider the following assertion [a] and reason [r] in the context of the load-elongation curves of fibres F1, F2 and F3
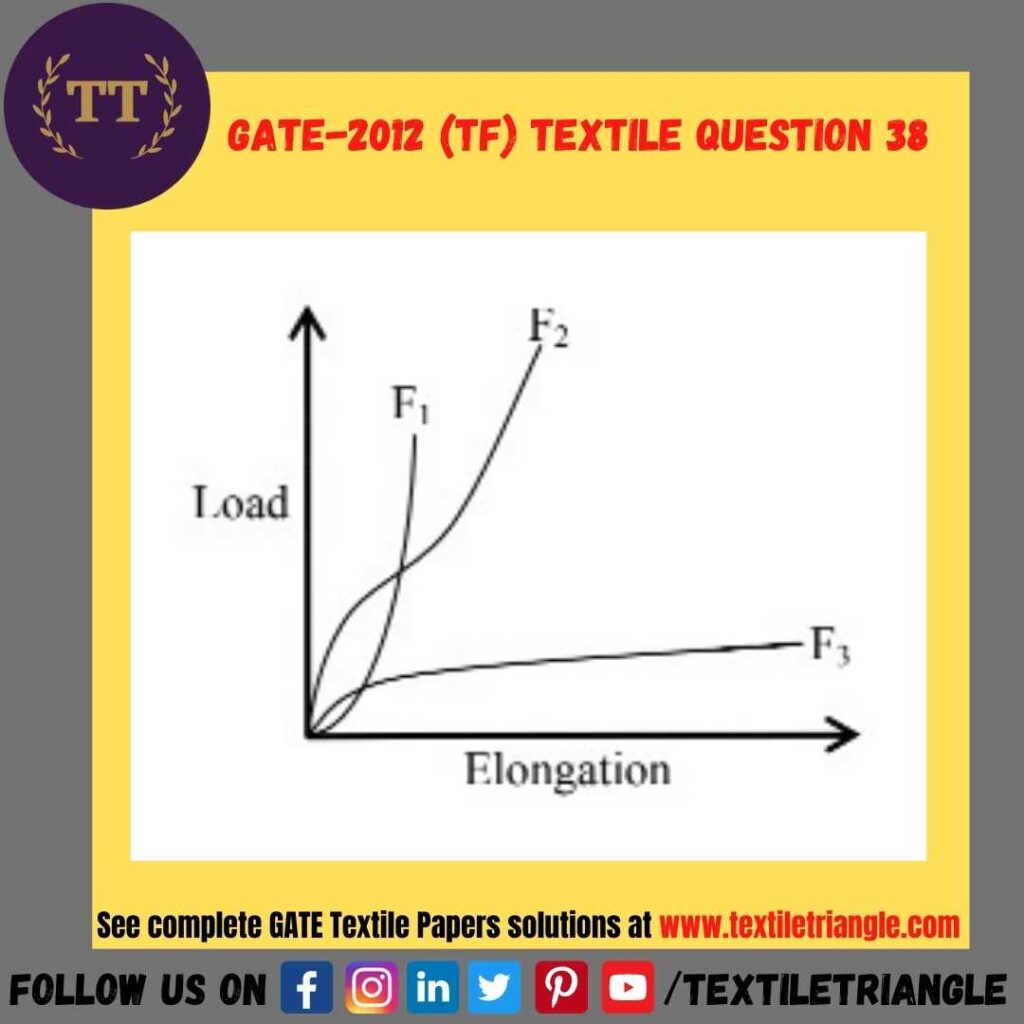
[a] Fibre F3 is the most suitable fibre for making a rope for mountaineering.
[r] Mountaineering rope should have high tenacity, high modulus and high work of rupture.
Determine the correctness or otherwise of the above Assertion [a] and Reason [r]
| (A) | [a] is right [r] is wrong |
| (B) | [a] is right [r] is right |
| (C) | [a] is wrong [r] is right |
| (D) | [a] is wrong [r] is wrong |
Answer / Solution
[Show Answer]
Option C
Frequently Asked Questions | FAQs
What is load elongation curve?
A load elongation curve, also known as a stress-strain curve or a tension curve, is a graphical representation of the mechanical behavior of a material under tensile loading. It shows the relationship between the applied load (stress) and the resulting elongation (strain) of the material.
The load elongation curve is typically generated by subjecting a sample of the material to tensile testing, which involves stretching the sample until it breaks while measuring the load and elongation at each stage. The resulting data is then plotted on a graph, with stress on the y-axis and strain on the x-axis.
The load elongation curve typically has several distinct regions:
Elastic region: In this region, the material behaves elastically, meaning that it returns to its original shape after the load is removed. The stress is directly proportional to the strain, and the slope of the curve (known as the Young’s modulus) is a measure of the stiffness of the material.
Yield region: At a certain point, called the yield point, the material begins to deform plastically, meaning that it undergoes permanent deformation when the load is removed. The stress in this region remains approximately constant while the strain increases.
Plastic region: Beyond the yield point, the material undergoes increasing plastic deformation as the load is increased. The stress in this region also increases as the strain continues to increase.
Fracture region: At a certain point, called the fracture point, the material breaks, and the load drops to zero. The strain at this point is a measure of the ductility of the material.
The load elongation curve provides valuable information about the mechanical properties of a material, including its stiffness, strength, and ductility. It is widely used in engineering and materials science to evaluate the suitability of materials for specific applications and to design structures that can withstand applied loads.
What is work of rupture in textile?
The work of rupture in textiles is a measure of the energy required to break a sample of a textile material under tension. It is also known as the breaking work or breaking energy.
The work of rupture is calculated by integrating the load-elongation curve up to the point of sample failure, which gives the area under the curve. This area represents the energy absorbed by the material during deformation and fracture.
The work of rupture is a useful measure of the tensile strength and toughness of a textile material. Tensile strength is a measure of the maximum load that a material can withstand before breaking, while toughness is a measure of the material’s ability to absorb energy before fracture.
In general, materials with higher tensile strength and toughness will have a higher work of rupture. This makes the work of rupture a valuable parameter in evaluating the performance of textile materials for various applications, such as in the production of high-strength fabrics or protective clothing.
The work of rupture can be influenced by various factors, such as the composition and structure of the textile material, the processing conditions, and the testing method. Therefore, it is important to carefully control these factors when measuring the work of rupture to ensure accurate and meaningful results.
