Question 03 (Textile Technology & Fibre Science)
The eigenvalues of the matrix 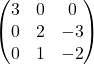 are
are
| (A) | -1, 1, 3 |
| (B) | -3, 2, -2 |
| (C) | 3, 2, -1 |
| (D) | 3, 2, 1 |
[Show Answer]
Write Here
A=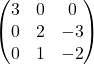
![]()
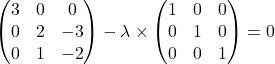
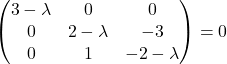
![]()
![]()
![]()
![]() (Ans)
(Ans)
These are the eigen values.
The eigenvalues of the matrix 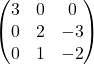 are
are
| (A) | -1, 1, 3 |
| (B) | -3, 2, -2 |
| (C) | 3, 2, -1 |
| (D) | 3, 2, 1 |
Write Here
A=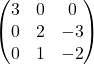
![]()
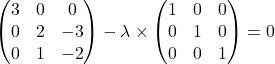
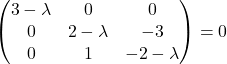
![]()
![]()
![]()
![]() (Ans)
(Ans)
These are the eigen values.